如图,在半圆O中,直径AB=10,AD=8,∠1=∠2,求AC的长度。这题怎么做呢?
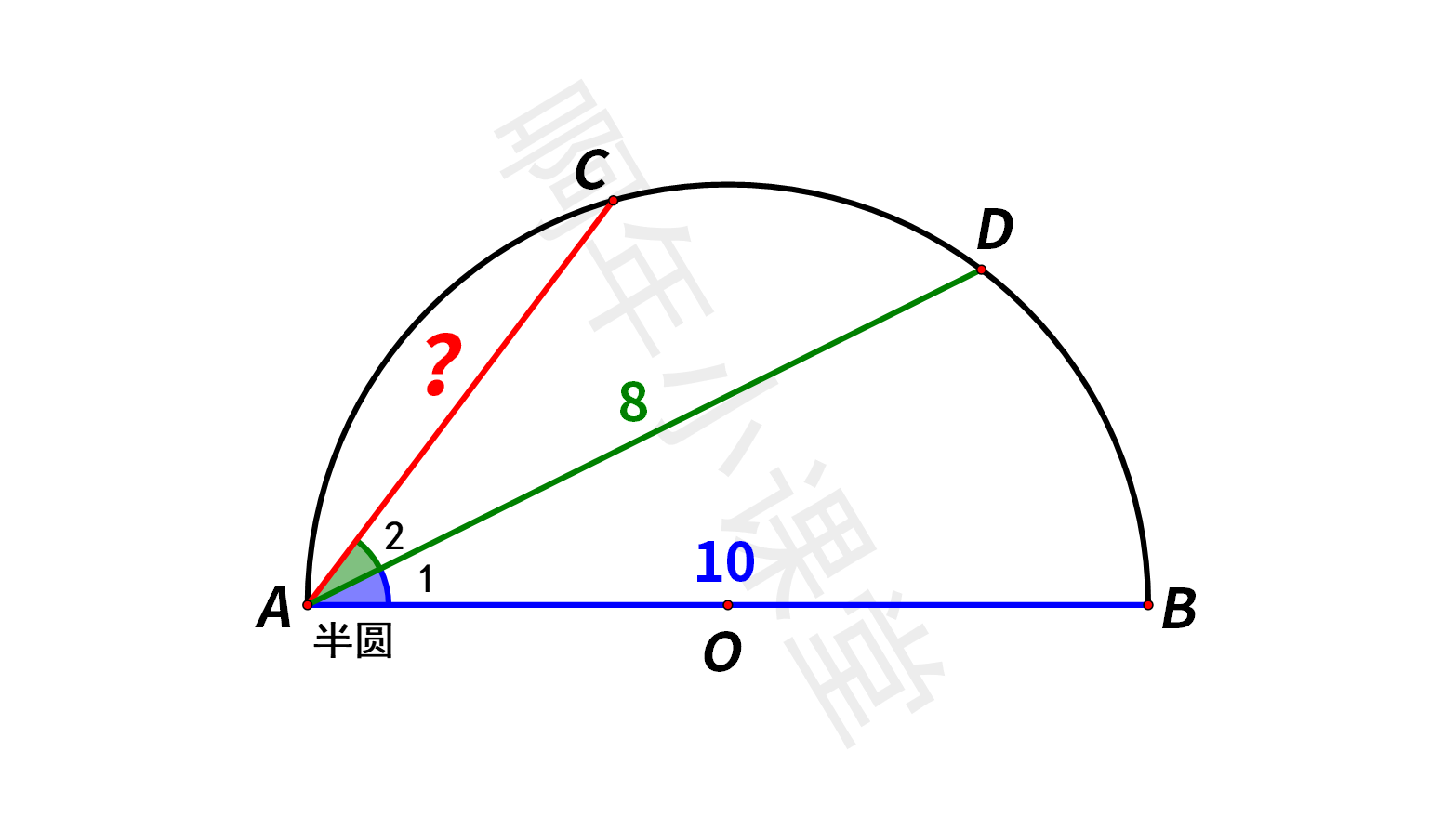
我们知道直径所对的圆周角为90°,不妨连接BD、BC,
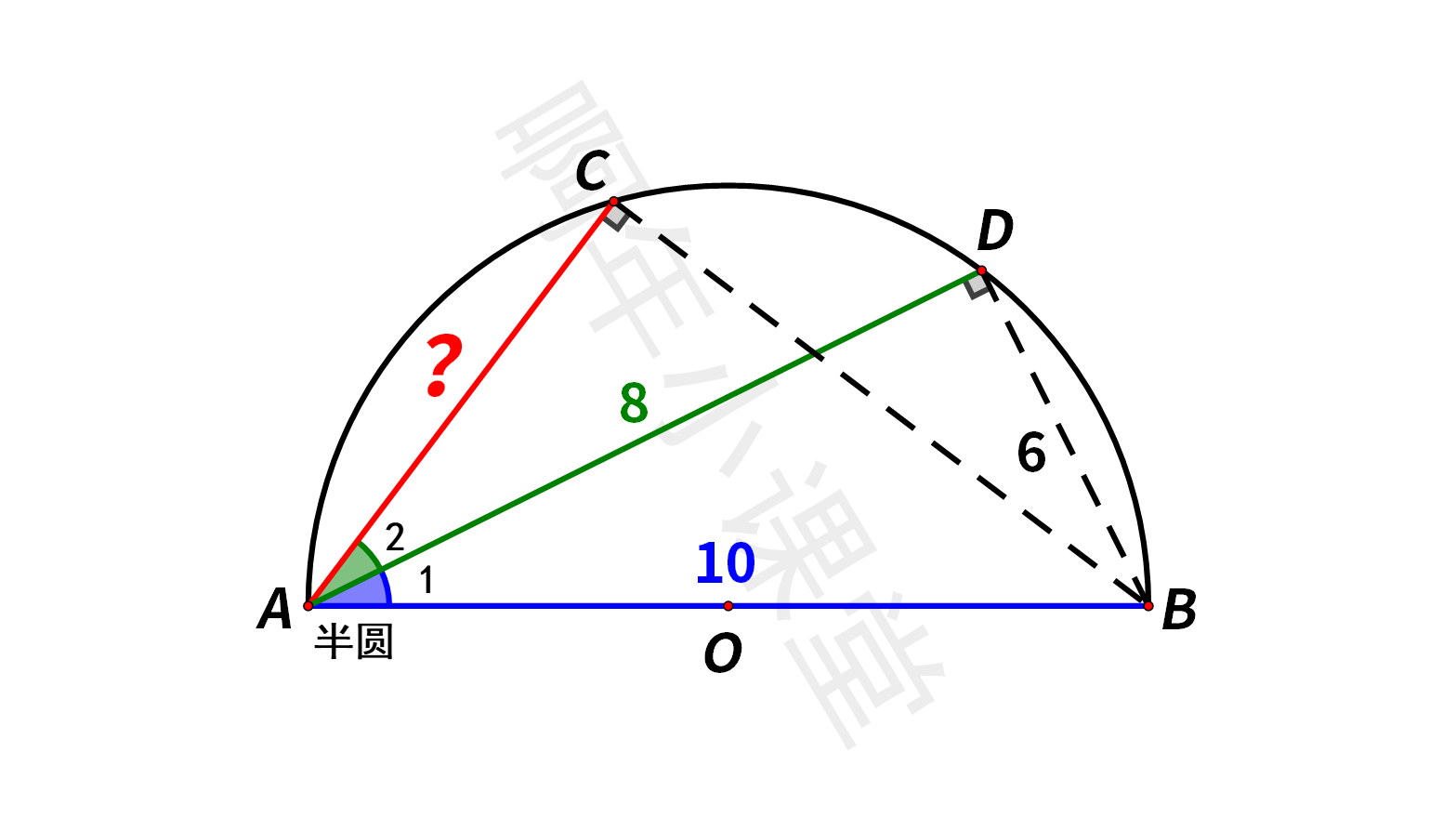
∠ACB=∠ADB=90°,
而AB=10,AD=8,
由勾股定理可得,BD=6。
接下来怎么做了呢?
我们要求的是AC的长度,题目条件∠1=∠2还没有使用。
∠1=∠2,AD是角平分线,看到角平分线,同学们想到了什么?
比较容易想到的是角平分线的性质:角平分线上的点到角两边的距离相等。
除此之外,我们也可以延长BD和AC,BD和AC的延长线相交于点E,
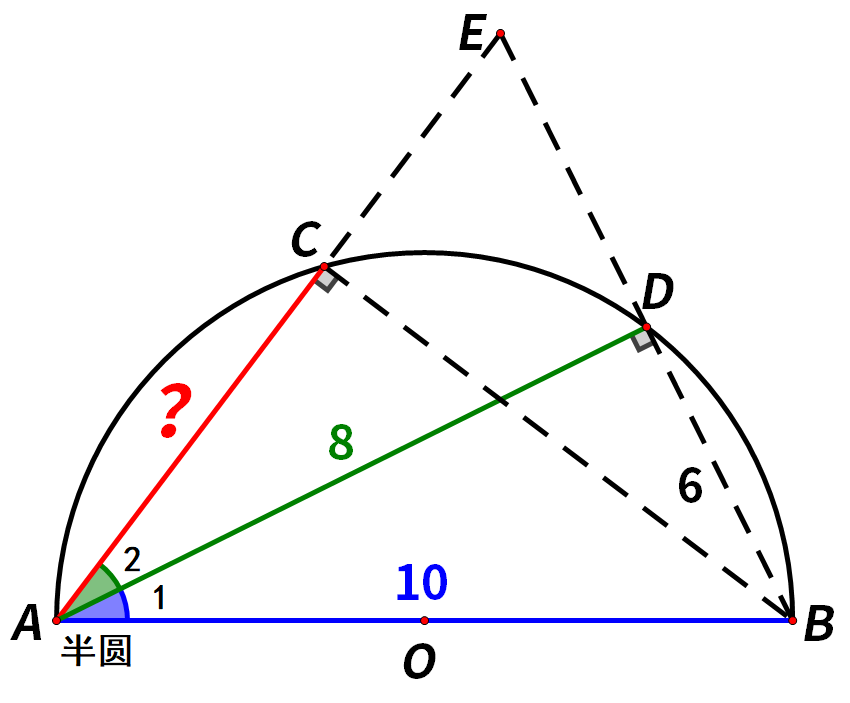
在三角形ADB和三角形ADE中,
∠1=∠2,
AD是公共边,
∠ADB=∠ADE=90°,
由角边角证全等可得三角形ADB和三角形ADE全等。
三角形ADB和三角形ADE全等,
DE=DB=6,AE=AB=10。
接下来我们看到三角形ABE,
三角形ABE的面积=BE×AD÷2=AE×BC÷2,
而BE=12,AD=8,AE=10,所以BC=48/5。
三角形ABC是直角三角形,AB=10,BC=48/5,
由勾股定理可得,AC=14/5。
文章版权声明:除非注明,否则均为藏品岁月痕原创文章,转载或复制请以超链接形式并注明出处。